既卒生:カリキュラム

無駄を省いた教材とカリキュラムで、偏りのない実力を育む

まずは単元別のテキストを用います。そこでは問題ごとにレベルが細かく設定され、生徒の学力に合わせた学習が進められます。またこのテキストから特に必須となる問題を１テーマ１問の形式で抜粋した「重要問題集」を併用することで、復習する際の優先順位が明確となり効率よく学習できます。

その他、より応用的な課題に取り組みたい人のための「実践問題集」、基礎計算力を強化したい人のための「補充問題集」など、実に多様な学力に応じた教材を用意しています。以下、時期ごとのカリキュラムの概要です。

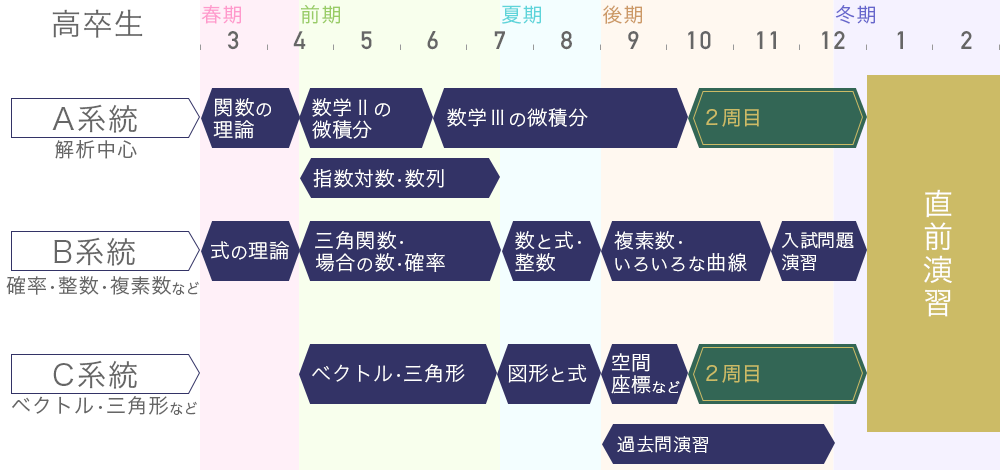
• 春期講習（3月〜4月）:高校数学の根幹をなす「関数」「式」の基本を学習。　
• 前期・夏期講習（４月〜８月）：数Ⅱ・Ⅲの微積分が主の解析系統と、幾何や確率を中心とした系統に大きく分け、単元別に進行。
• 後期講習（９月〜12月）：単元別の１巡目のテキストは10月頃に終了。その後は「重要問題集」で基礎の抜けを埋めつつ、入試レベルの問題を単元ごとに集めた「２巡目テキスト」、医学部の過去問で年々更新される「入試問題演習」などで実戦力を強化。またこの時期に、テスト形式で過去問演習を実施。
• 冬期・直前講習（12月〜２月）：前述の後期のテキストと並行して、「基本事項のチェック」で最終的な知識を確認、大学別直前テキストで最終的な仕上げ。

Point:多様なニーズに柔軟に対応できる教材作成力。過去問の解答も充実。

前述した全生徒共通のテキスト以外に、個々の生徒に対して講師の発案や生徒からの要望に応じた教材もすぐに用意できます。分野、難易度、出典などから問題を即座に選別するシステムを用い、さらに経験豊かな講師の目によって厳選された教材を提供します。また医学部入試の過去問について、解答速報を実施している大学はもちろんのこと、その他の大学についても独自の解答・解説を用意しています。

高校3年生:指導方針

視野を広げるテキストと一人ひとりへのきめ細かい指導で得点力をアップ

　難化を極める現在の医学部入試では、数学が合否のカギを握っています。単に教科書的な出題は減り、解法の丸暗記では歯が立たない問題が増えています。必要なのは、深い理解と精度の高い計算力、すなわち「真の数学力」なのです。

　そのために、メビオでは既成の枠組みを越えて論理のつながりに注目したテキスト体系を作り上げました。基礎を学ぶ段階では、時には中学レベルのグラフを描く作業からスタートします。入試数学にいち早く到達するためには、かえってそれが近道なのです。一方で応用力養成の授業では、数学の深い部分でのつながりを重視し、分野を横断して解法を探る力を鍛えていきます。

　授業は決して講師から生徒への一方通行ではありません。授業の中で、生徒本人にしっかり手を動かしながら問題を解いてもらいます。講師はその様子をつぶさに観察し、的確な指摘や指示を与えます。生徒が「わかったつもり」に陥ったままでは「真の数学力」は身につきません。必ず正確なアウトプット（公式や知識の運用）ができるようにきめ細かく指導します。

高校3年生:カリキュラム

無駄を省いた教材とカリキュラムで、偏りのない実力を育む

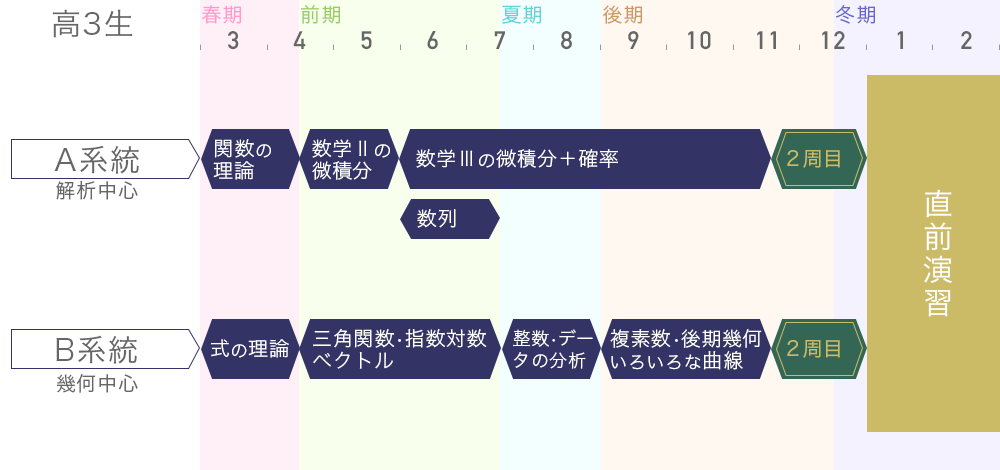
　既卒生に比べ時間に余裕のない高3生のために、より効率化を図った専用のテキストを使用します。また週3コマのうち1コマを「演習」に特化し、無理のないペースで確かなアウトプット力を会得できるよう配慮しています。

　年度の前半〜中頃は単元別のテキストを用います。そこでは問題ごとにレベルが細かく設定され、生徒の学力に合わせた学習が進められます。また必須問題を１テーマ１問の形式で抜粋した「重要問題集」を併用することで、復習の優先順位が明確となり効率よく学習できます。その他、発展問題に取り組みたい人向けの「実践問題集」、基礎計算力の強化を目的とした「補充問題集」など、多様な教材を用意しています。

　単元別のテキストは11月頃に終了し、その後は「重要問題集」で基礎の抜けを埋めつつ、入試レベルの問題を集めた「２巡目テキスト」や医学部の過去問演習で実戦力を強化します。さらに12月〜2月には、「基本事項のチェック」で知識を再確認、大学別直前テキストで最終的な仕上げを行います。

数学が苦手なのですが、おすすめの勉強方法を教えてほしいです。

受験数学を解くにあたっては、前提となる知識が必要です。
「センスがない」と悩む受験生は多いですが、問題が解けないのは、センスがないからではなく実は解法を知らないから、ということはよくあります。まずは基本知識や解法の習得に努めましょう。単に公式や解法を丸暗記するのではなく、「～という状況だからこの解法を使う」といった説明が言えるようにすることを心掛けましょう。
また、模範解答を読んだり授業で解説を聞いたりするだけでなく、必ず手を動かして自分で答案を作ってみましょう。理解したつもりでも、いざ自分で答案を作ろうとしてみたら途中で詰まってしまう、ということは必ずと言ってよいほど起こるものです。しっかり自力で答案が書けるようになるまで繰り返し解きましょう。
ただし、しっかり理解した上で答案が書けているかどうかは、自分自身では判断がつかない場合もあると思います。可能であれば、学校や予備校の先生に自分の手元（答案を作る様子）を見てもらうのが望ましいです。メビオでは少人数クラスでの授業ですので、そういったチェックを常時実施しています。

高校時代は文系だったので数学IIIを履修していませんが、大丈夫でしょうか？

不安を感じるのは無理もありません。確かに数学Ⅲでは、それに先だって学習する数学ⅠAⅡBの内容を踏まえた上で、さらに高度な内容を扱っていきます。しかし、練習量次第で得点力を向上させやすい面があります。特に数学Ⅲの微積分ではその傾向が顕著です。そして、この「練習量」を満足に確保できていない受験生は意外に多く存在します。文系だったことはハンディであるとは言え、今後の練習次第で他の受験生と互角に戦えるレベルに達することは十分可能です。メビオでは、文系出身から医学部合格を勝ち取った生徒は毎年のようにいます。ゼロから指導しますので大丈夫です。

過去問対策はいつから始めるのがよいでしょうか？

早めに始めるに越したことはありませんが、前提となる基本が未習得のままチャレンジしても当然歯が立ちません。まずは基本事項を少なくとも1周してから始めましょう（メビオでは、10月くらいから過去問演習をスタートさせます）。過去問は、その大学の出題傾向や難易度を知るために有効です。また、単に出題の雰囲気に慣れておくだけでも試験本番でプラスに作用するでしょう。
ただし、私立大学医学部の過去問を解くにあたっては注意してほしいことがあります。それは、かなりの学力をもっている受験生でも「制限時間内に解ききる」「高得点をとる」ということが難しい場合が多々あるということです。どの問題を時間内に正解すればよいのか、という見極めは自分では難しいと思います。学校や予備校の先生に相談してみるのがよいでしょう。メビオでは、多くの生徒が受験する大学の過去問を中心に、そういったアドバイスを生徒に伝えています。

国公立大学医学部志望ですが、私立大学医学部にも興味があります。数学の勉強の仕方で気をつけておくべきことはありますか？

私立大学医学部の入試数学は、国公立に比べるとクセのある出題が多いです。あらかじめ過去問を何年分か見ておいた方がよいでしょう。また、マークシートや空所補充などの「答だけを問う出題形式」であったり、分量が多い場合がよくあります。すばやく正確な計算力を身に付けておくことも重要です。

公式がなかなか覚えられないのですが、どうすればよいでしょうか？

公式を文字だけで覚えようとしていませんか？　
たとえば三角形に関する公式（余弦定理や中線定理など）であれば、三角形の図をイメージした上で、各文字が図中の何に対応しているかを意識しながら覚えるとよいでしょう。公式の導出過程を何度もなぞってみることも有効です。式の意味についての理解が深まり覚えやすくなります。また、単に公式を目にする機会を増やしてみるのもよいでしょう。
そういうときのために、メビオ数学科では教材「チェックリスト」を用意しています。メビオ生ならぜひ活用してくださいね。

計算ミスがなかなか減らないのですが、どうすればよいでしょうか？

メビオの今までの例から見て、式変形の行を省略する人は間違いが多いです。移項と展開と整理を同時にしてしまうと、見直したときにも間違いに気付きません。式の行はあまり節約しないようにしましょう。
また、字の乱雑すぎる人、計算を書き散らす人も間違いが多いです。計算は後から直すのではなくて一度で合わせるつもりでしてください。
計算ミスの傾向は人によって異なりますので、ミスを減らすには「自分がどのようなミスをするのか」を認識することが大切です。そのために、ミスを記録するノートを作っていくことも有効でしょう。

計算練習をしたいのですが、大学入試用の計算ドリルがあまり売っていません。計算力をつけるには、どうやって対策すればよいですか？

計算力をつけるにはやはり練習を多く積むことが重要です。
市販でいくつか練習書（たとえば数研出版の教科書傍用問題集など）が出版されていますので、それを使って練習するとよいでしょう。ただし、無闇に練習するのではなく、適切で要領のよい方法で計算していくことが重要です。参考書に載っている計算過程をじっくり確認しましょう。あるいは、学校や予備校の先生に自分の計算過程を見てもらえると手早いでしょう。もちろんメビオでは、各生徒の計算の様子をつぶさにチェックしています。また、計算練習のための独自の教材も用意しています。

図形問題が昔から苦手です。中学範囲にさかのぼって勉強したほうがよいですか？　特に相似が苦手です。

医学部の入試では、幾何分野は頻出です。中学の範囲が弱いのであれば、ぜひさかのぼっておさらいしましょう。メビオでも、通常カリキュラムで早い時期に中学の範囲の幾何を学習することになっています。

確率が苦手です。どのように勉強すればいいか教えてください。

参考書や問題集を見て正しい解答を読み、納得することも大切なのですが、それと同じくらい、いやむしろそれ以上大切なことがあります。
「自分の作った計算式がなぜ間違ったかを考え、理解すること」です。
自分の出した答が正解より大きければ、なぜ大きすぎたのか。正解より小さければ、なぜ小さすぎたのか。そのことを毎回きちんと考えて納得するようにしないといけません。自分が作った誤答をしっかり分析しないといけません。自分の誤りの原因をしっかり究明して同じ誤りを繰り返さないようにしないといけません。
これはどの分野でも大切なことですが、特に「場合の数」「確率」の分野ではより大切になります。なぜなら「場合の数」「確率」の分野での誤答は、思いこみから式を作ってしまうことにあるからです。その思いこみが、なにをどう間違っているかを把握しないと、いつまでもその思いこみから脱却できないのです。
ですので、間違えた問題を「なぜ間違えたか」しっかり分析してください。もちろん学校、塾、予備校など、使えるものは大いに利用しましょう。

学校の先生から、青チャートを使って何度も解きなさいと言われます。メビオでも青チャートは使いますか？

メビオでは、青チャートに限らず市販のテキストはほとんど使用せず、オリジナルの教材を使っています。
どんな教材を使うにせよ、繰り返し解くことは有効です。ただし、「答えを覚えているから何となく解ける」では困ります。なぜその解法を使うのか、などを言葉で説明できるように心掛けるとよいでしょう。

学校の授業進度が遅いので独学で高校数学を勉強しているのですが、どの分野・どの単元からどのような順番で勉強すれば、効率よく勉強できますか？

医学部の受験では、ほとんどの場合「数学Ⅲの微積分」が出題されます。
この分野を習得するならば、それに先だって「数と式①、2次関数②（以上数学Ⅰ）」「いろいろな式③、三角関数④、指数対数⑤、微分積分⑥（以上数学Ⅱ）」「数列⑦（数学B）」を学習する必要があります。
学習する単元の順序としては、＜①②＞→＜③＞→＜④～⑦＞となります。それぞれの＜＞の中については順序は特になく、複数の単元を並行して進めてもよいでしょう。
これらすべてをミッチリと学ぶのが難しい場合は、②と⑥の比重を大きくし、それ以外については教科書に載っている基本事項をおさらいしておきましょう。

また、幾何的な分野も医学部では頻出です。
単元名を挙げると「図形と計量⑧（数学Ⅰ）」「図形の性質⑨（数学A）」「図形と方程式⑩（数学Ⅱ）」「ベクトル⑪（数学B）」となります。高校ではこの順で学ぶことが多いでしょう。独学で勉強する場合もそれでよいと思います。どの分野も重要ですが、特に頻出な単元は⑨と⑪です。どうしても時間がない場合はこの2つを優先しましょう。ただしメビオでは⑪を優先的に学んでいます。それによってその他の単元での理解がスムーズになる面があるからです。
「場合の数と確率（数学A）」も医学部入試で頻出です。他の単元との関連は低いので、単独で勉強を始めやすいと思います。経験的に言ってこの単元は得点力を身に付けるのに時間が掛かる人が多いので、なるべく早く始めましょう。他の単元と並行して少しずつ進めていくのがおすすめです。
その他についてですが「データの分析（数学Ⅰ）」は学ぶ順序について特に制約はありません。「複素数平面、いろいろな曲線（以上数学Ⅲ）」は、あらかじめ「図形と方程式」「三角関数」「ベクトル」を学んでおくことが望まれます。

再受験生ですが、複素数平面など高校の頃に習っていない範囲があります。新指導要領で、気をつけてをおくべきテーマを教えてください。また、メビオではゼロから教えていただけますか？

現行課程から新たに扱われるようになったのは、「データの分析（数学Ⅰ）」「条件付き確率、整数（以上数学A）」「複素数平面（数学Ⅲ）」などです。メビオでは、もちろんこれらの内容をゼロから学んでもらいます。