2021大医後期 的中のフカヨミ|メビオ化学科 講師 関根
2021大医後期 的中のフカヨミ|メビオ化学科 講師 関根
うんちく・小ネタ
入試
メビオ講師コラム
2021/04/08(木)
(最終更新日2023/02/04)
2021大医後期 的中のフカヨミ
メビオ化学科の関根です。今日は、2021年度大阪医科大学後期日程(3月10日実施)の入試問題についてお話をさせていただきます。
この問題はメビオの直前授業にてみごと「ズバリ的中」を果たした設問だったわけですが、この文章では、入試問題と授業で扱った問題の比較をもとにして、受験生が取るべき化学の勉強法と、問題の内容についてのちょっとだけ深い理解について考えてみたいと思います。
受験学年でない方や、化学はちょっと苦手・・・という方は、それぞれの問題文の中身は流し読みしながら読み進めていただいても構いません。
的中内容の見比べ
まずは、2021年3月10日に出題された問題文と、同3月2日にメビオの授業で扱った内容を見比べてみましょう。
大問Ⅰの設問は以下のようなものでした。解答に必要な情報が前半に書かれており、下線部について考える問1から始まる誘導に従って、問5までが順序立てて考えられるように構成されています。
2021年度大阪医科大学一般選抜後期試験 大問Ⅰ
酵素はタンパク質を主成分とした触媒であり,常温常圧という穏やかな条件下でも速やかに化学反応を進行させることができる。
$\mathrm{E}$ を酵素,$\mathrm{S}$ を基質,$\mathrm{ES}$ を酵素と基質が結合した酵素ー基質複合体,$\mathrm{P}$ を生成物とすると,この酵素反応は,$\mathrm{E + S} \ \rightleftarrows \ \mathrm{ES} → \mathrm{E} + \mathrm{P}$ で表すことができる。[$\mathrm{E}$],[$\mathrm{S}$],[$\mathrm{ES}$],[$\mathrm{P}$] をそれぞれ $\mathrm{E}$,$\mathrm{S}$,$\mathrm{ES}$,$\mathrm{P}$ の濃度とする。まず,$\mathrm{E}$ と $\mathrm{S}$ から $\mathrm{ES}$ が生成する過程の反応速度は $v_1 = k_1 \mathrm{[E][S]}$ であり,その逆反応の反応速度は $v_2 = k_2 \mathrm{[ES]}$,そして $\mathrm{ES}$ から生成物 $\mathrm{P}$ が生成する過程の反応速度は $v_3 = k_3 \mathrm{[ES]}$ となる。ただし,$k_1$,$k_2$,$k_3$ は,それぞれの反応の速度定数であり正の値をとる。
この反応では$\underline{任意の時刻において単位時間内に \mathrm{ES} が生成する量と消滅する量が等しくなる}$ことが知られている。また,基質を結合していない酵素と結合している酵素の濃度の和 $\mathrm{[E]_T = [E] + [ES]}$ は $\mathrm{[S]}$ や時刻に関係なく一定である。以下の問に答えよ。
なお,問 2 ~問 5 は $k_1$,$k_2$,$k_3$,$[\mathrm{E}]_\mathrm{T}$,$[\mathrm{S}]$ の中から必要なものを用いた式で表すこと。
- 問 1
- 下線部より $v_1$,$v_2$,および $v_3$ の間に成り立つ式を示せ。
- 問 2
- 問1の結果を用いて $\mathrm{[ES]}$ を式で表せ。
- 問 3
- $\mathrm{P}$ が生成する速度を式で表せ。
- 問 4
- $\mathrm{[S]}$ を限りなく増加させると,問 3 の速度はある極限値に収束する。その値を式で記せ。
- 問 5
- 問 3 の値が問 4 の値の $\dfrac{1}{2}$ となるときの $\mathrm{[S]}$ を式で示せ。
対して、メビオの授業で3月2日に扱った問題は以下のとおりです。
メビオ直前授業 2021 年 3 月 2 日 テキスト
この反応は可逆反応であり, $\mathrm{A}$,$\mathrm{B}$,$\mathrm{C}$ の各濃度を $[\mathrm{A}]$,$[\mathrm{B}]$,$[\mathrm{C}]$ とすると,正反応の反応速度は $k_1 \mathrm{[A][B]}$ で表され,逆反応の反応速度は $k_2 \mathrm{[C]}$ で表される.ここで $k_1,k_2$ は反応速度定数である.反応開始時は, $\mathrm{[A]} = a$,$\mathrm{[B]} = b$,$\mathrm{[C]} = 0$ であった.ただし, $a$ の値は $b$ の値に比べて十分大きく, $a − b \fallingdotseq a$ と見なすことができる.
以下の問いに $k_1$,$k_2$,$k_3$,$a$,$b$ の記号を組み合わせた最も簡潔な式で答えよ.
- 問 1
- 反応 1 は反応開始後速やかに平衡状態に達した.このときの平衡定数(濃度平衡定数)を求めよ.
- 問 2
- 平衡状態に達したときの $\mathrm{C}$ の濃度を求めよ.
詳しく観察すると,反応 1 に比べるときわめてゆっくりとした反応ではあるが, $\mathrm{C}$ は分解して $\mathrm{B}$ と $\mathrm{D}$ が生成することが明らかになった.この反応を反応2 と呼ぶ.
$\hspace{2cm} \mathrm{C} \longrightarrow \mathrm{B} + \mathrm{D} (反応2)\\$反応 2 は不可逆反応で,その反応速度は $k_3 \mathrm{[C]}$ で表される.ここで $k_3$ は反応速度定数である.
- 問 3
- $\mathrm{D}$ が生成する反応速度を求めよ.ただし,反応 $1$ はすでに平衡状態に達しており,かつ $\mathrm{D}$ の濃度は $a$ に比べて十分小さく, $a − [D] \fallingdotseq a$ と見なすことができる.
- 問 4
- $b$ の値を一定に保ったままで $a$ の値を限りなく増加させると $\mathrm{D}$ の生成速度は一定の値に収束する.この値を $v_\mathrm{max}$ とする. $v_\mathrm{max}$ の値は $\mathrm{B}$ の初期濃度を $b$ としたときの $\mathrm{D}$ の生成速度の最大値となる.この $v_\mathrm{max}$ の値を求めよ.
- 問 5
- $\mathrm{A}$ と $\mathrm{B}$ が反応して $\mathrm{C}$ になりやすければ, $a$ の値が小さくても $\mathrm{D}$ の生成速度が大きくなる.この $\mathrm{C}$ になりやすさの指標は, $\mathrm{D}$ の生成速度が $\dfrac{v_{\max}}{2}$ となる $a$ の値で表すことができる.この指標となる $a$ の値を求めよ.
授業で扱った問題も同じ大阪医科大学の2017年度前期日程にて出題された問題だったのですが、
これらを見て「同じ内容だ!」と思えたでしょうか?
すぐにそう感じることが出来た方は、しっかり化学の勉強をしてきた方だと思います。
どちらの設問も、前提知識があまりなくとも問題文の指示に従って解答する、いわゆる『読解力および思考力を問う問題』のように見えますが、実はどちらも(少し気の利いた問題集には収録されている)酵素基質反応の反応速度を扱っている内容なのです。
過去問をやり込めば対策として充分?
このように,私立医学部の入試問題では、過去問と同じテーマを扱う出題がなされることが少なくありません。
では、「第一志望校の過去問をやり込めば対策として充分である」ということでしょうか?
それを考えるためにも、上述の質問をもう一度振り返りたいと思います。
2017年度の設問では「酵素」「基質」といった用語が登場しない分、その本質的な部分が見えづらい出題となっていました。
果たして単に過去問演習に取り組んでいた受験生がこれら2つの設問の本質的な共通点に気づけたかどうかというと、自力では難しかったのではないかと思われます。
おそらく2017年度の過去問に触れたほとんどの受験生が、「単に問題文の指示に従って答えだけは合わせられるようにした」という段階で留まってしまったのではないかと予想されます。
実は同じテーマ(酵素基質反応の反応速度)は、2014年度の関西医科大学後期日程や、国公立大学では2020年度の神戸大学、2016年度の山梨大学でも出題されています。
一方で、大阪医科大学では2017年度より前においては、手元で確認できる限り過去30年以上は出題されていません。
また当然ながら、2021年度入試において大問Ⅰだけを解けたとしても合格点には達しません。
その他の3題についてもしっかりと得点することが求められたはずです。
これらのことをふまえると、医学部合格のためには、単に過去問をやり込むだけではなく、どの大学にも対応できるようなユニバーサルな勉強が求められることがうかがえます。
後期試験 大問Ⅰ掘り下げ
最後に、2021年度後期の大問Ⅰに関して少し内容を掘り下げておきましょう。
(解答速報には『(参考)』として記した内容ですが、ここではグラフも考えてみたいと思います。)
酵素基質反応においてはまず、酵素($\mathrm{E}$)と基質($\mathrm{S}$)が反応し、酵素基質複合体を形成します。
$\hspace{2cm}\mathrm{E + S} \longrightarrow \ \mathrm{ES}$その後、酵素基質複合体が反応を起こし、生成物($\mathrm{P}$)と酵素($\mathrm{E}$)が生成します。
$\hspace{2cm}\mathrm{ES} \longrightarrow \ \mathrm{E + P}$1 つ目の反応の正逆の速度定数を$k_1$および$k_2$、2つ目の反応の速度定数を$k_3$、反応系に加えた酵素の総濃度を $\mathrm{[E]}_\mathrm{T}$ とすると、ここでの生成物($\mathrm{P}$)の生成速度 $v$ が,$v=\dfrac{k_1k_3[\mathrm{E}]_{\mathrm{T}}[\mathrm{S}]}{k1[\mathrm{S}]+k_2+k_3}$ $\cdots$ (*) と表されることが問 3 の結果からわかりました.
また、この式において$[\mathrm{S}] \to \infty$ とすることで、反応速度が最大値$v_{\mathrm{MAX}}=k_3[\mathrm{E}]_{\mathrm{T}}$に漸近することが問4からわかりました。
これを単に「酵素基質反応の反応速度はある値以上に速くならないんだ」という(問題文通りの)理解に留まらず、この現象についてもう少し深く考えてみましょう。
(*) の式を少し変形して、
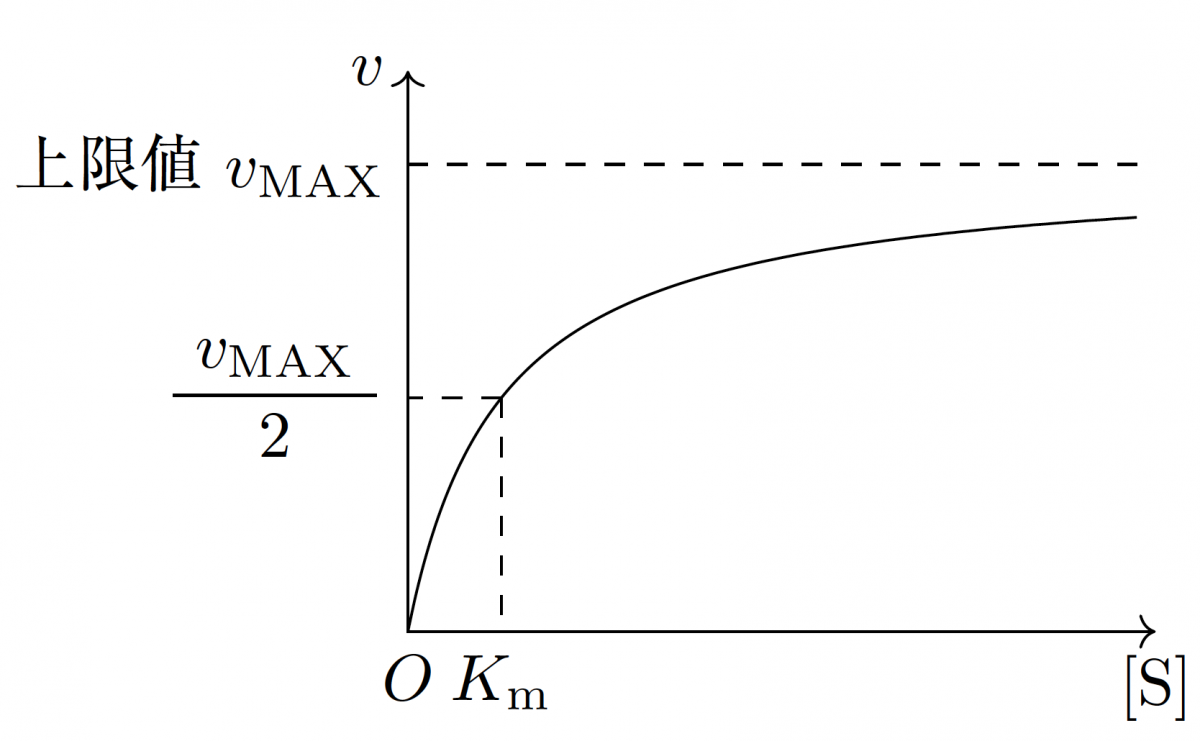
これを、横軸に基質濃度 $[\mathrm{S}]$ 、縦軸に $\mathrm{P}$ の生成速度 $v$ をとってグラフ化すると次のような形になります。
このような酵素基質反応の反応速度を表す式をミカエリス・メンテン式とよび、 $K_\mathrm{m}$ の値をミカエリス定数とよびます。
上式のとおり、ミカエリス定数は反応速度が$\dfrac{v_{\mathrm{MAX}}}{2}$になるときの基質濃度に一致するため、酵素と基質の結合の起こりやすさを表す定数として、その酵素の触媒能力の一つの指標となっています。
また、グラフおよび式の特徴として、
- 酵素濃度 $\mathrm{[E]}_\mathrm{T}$ に比べて基質濃度 $\mathrm{[S]}$ が小さい領域では、生成物 $\mathrm{P}$ の生成速度 $v_3$ はほぼ $[\mathrm{S}]$ に比例する。
- 酵素濃度 $\mathrm{[E]}_\mathrm{T}$ に比べて基質濃度 $\mathrm{[S]}$ が大きくなると、生成物 $\mathrm{P}$ の生成速度 $v_3$ は一定値 $v_{3,MAX} = k_3\mathrm{[E]}_\mathrm{T}$ に漸近していく。
ということもあわせて知っておくと、酵素基質反応に対してより理解が深まることと思います。
イメージとしては、スーパーのレジや遊園地のチケット売り場などを思い浮かべると良いかもしれません。
すなわち、
- レジの数に比べてお客さんが少ないときは、買い物を終えて店から出ていくお客さんの数はほぼお客さんの数に比例する。
- レジの数に比べてお客さんが多くなると、(レジ待ちの列が出来て)買い物を終えて店から出ていくお客さんの数は一定値に漸近していく。
という感じでしょうか。
$\mathrm{[E]}_\mathrm{T}$ がレジの数、 $[\mathrm{S}]$ がお客さんの数、 $v_3$ が店から出ていくお客さんの数ですね。
このように、式の上での扱いをただそのまま理解するのではなく、起こっている現象を身近なものとして捉えられるようになることこそ、受験化学の得点力アップの一つの要点だと思います。
他の色々の分野についても、ぜひそんな視点で勉強してみてください。
医学部進学予備校メビオ 化学科 講師 関根